Locality-Sensitive Hashing (LSH) is a groundbreaking technique for fast similarity search in high-dimensional data, revolutionizing applications from recommendation systems to genomics. This guide dives deep into LSH—its mechanics, math, variants, and real-world uses—making it the definitive resource for “LSH” and “local sensitive hashing” (a frequent search variant). Whether you’re a beginner or expert, explore interactive examples, comparisons, and more to master LSH.
What is Locality-Sensitive Hashing (LSH)?
LSH is an algorithm that hashes similar items into the same buckets with high probability, enabling efficient approximate nearest neighbor (ANN) searches in big data.
Introduction
Locality Sensitive Hashing (LSH) refers to a set of algorithmic techniques used to speed up the search for neighbours or duplicate data in the samples. LSH can be used to filter out duplicates in a database, scrape web pages or any websites at an impressive speed.
Introduced in 1998 by Indyk and Motwani (arXiv:cs/9812008), LSH tackled the “curse of dimensionality” in nearest neighbor searches. Variants like MinHash (Broder, 1997) and SimHash (Charikar, 2002) followed, with modern uses in vector databases (e.g., Faiss) and LLMs reflecting its 2025 relevance (Nature, 2024).
In computer science, LSH can be referred to as a technique that hashes similar input items into the same “buckets” with a high probability.
It differs from conventional hashing techniques in that hash collisions are maximised, not minimised. LSH technique can also be seen to reduce the dimensionality of high-dimensional data while preserving relative distances between items.
LSH maps high-dimensional data into buckets using hash functions that prioritize collisions for similar items:
How Does LSH Work?
- Hashing: Functions ensure similar points (e.g., based on Euclidean distance) collide.
- Bucketing: Groups similar items, shrinking the search space.
- Querying: Checks only the query’s bucket, not the entire dataset.
LSH functions are specifically designed so that hash value collisions are more likely for two input values that are close together than for inputs that are far apart. The term “close together” means that the data points that are within a certain distance bounded by a threshold value.
There are multiple hash functions for different use cases as there are multiple different LSH functions for different data types.
LSH algorithm can be implemented in languages such as Java and Python. Below are some of the libraries that can be used to implement LSH:
- java-LSH – This library implements Locality Sensitive Hashing (LSH), as described in “Mining of Massive Datasets”. Five different computations can be performed MinHash, Super-Bit, Comparable signatures, Initial seed and Serialization.
- LSH – This is a Python implementation of LSH using MinHash to detect near-duplicate text documents.
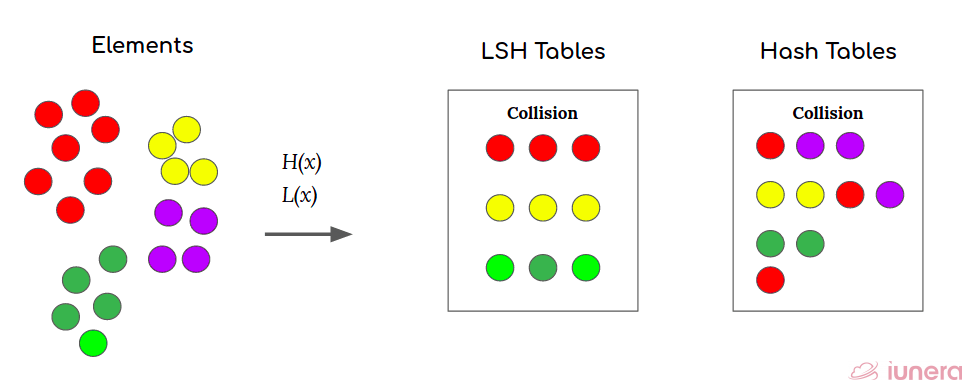
Hash functions map objects to numbers or bins. The LSH function L(x) tries to map similar objects to the same hash bin and dissimilar objects to different bins.
The key intuition behind LSH is that LSH functions try to group similar elements together into hash bins.
Mathematical Foundations
LSH’s power lies in its probabilistic design. A hash function ( h ) is locality-sensitive if:
- For d(x,y)>crd(x, y) > cr
d(x, y) > cr(where c>1c > 1c > 1), P[h(x)=h(y)]≤p2P[h(x) = h(y)] \leq p_2P[h(x) = h(y)] \leq p_2, with p1>p2p_1 > p_2p_1 > p_2. - For d(x, y) greater than c times r (where c is greater than 1), the probability P[h(x) = h(y)] is less than or equal to p_2, with p_1 greater than p_2.
Key Concepts of LSH
- Distance Metrics: Adapts to Euclidean (L2L_2
L_2), cosine, Jaccard, etc. - Random Projections: For Euclidean LSH, a random hyperplane v (Gaussian-distributed) splits space: h(x) = sign(v * x). Similar points (with a small angle) tend to align.
- Amplification: Combine k hash functions into a band, use L bands: P[collision] = 1 – (1 – s^k)^L, where s is similarity.
- Example: At s=0.8s = 0.8
s = 0.8, k=10k = 10k = 10, L=5L = 5L = 5, collision probability is ~99%.
LSH Hash Collision
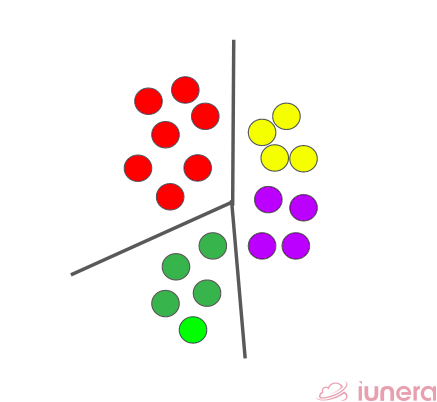
A hash collision occurs when two objects x and y have the same hash value. In our example above, all of the red dots collided, but this was not guaranteed to happen.
Under LSH, the term referring to how 2 data points are set to collide or have a chance to collide is “collision probability”. In a more mathematical notation,
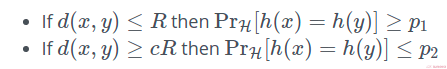
To summarise the equation above, given a distance function d(x,y) and a threshold value of R, if the distance is less than the threshold value, there is a good chance (probability > p) of collisions happening.
Types and Variants of LSH
| Variant | Distance Metric | Use Case |
|---|---|---|
| MinHash | Jaccard similarity | Text deduplication |
| SimHash | Cosine similarity | Document/image similarity |
| Random Projection LSH | Euclidean distance | Vector clustering |
| p-Stable LSH | L_p norms | Flexible ANN search |
| Multi-Probe LSH | Euclidean/Cosine | Reduces hash tables |
| Entropy-Based LSH | Various | Adaptive similarity search |
- Multi-Probe LSH: Probes multiple buckets to improve recall, reducing memory (e.g., used in Faiss).
- Entropy-Based LSH: Adjusts hashing based on data distribution, enhancing accuracy.
Interactive Examples
Example 1: MinHash LSH in Python
Find similar text documents:
from datasketch import MinHash, MinHashLSH
from nltk.tokenize import word_tokenize
docs = [
"Locality sensitive hashing is great",
"Locality hashing is really great",
"Totally different content"
]
lsh = MinHashLSH(threshold=0.7, num_perm=128)
minhashes = []
for i, doc in enumerate(docs):
m = MinHash()
for word in word_tokenize(doc):
m.update(word.encode('utf8'))
minhashes.append(m)
lsh.insert(f"doc{i}", m)
result = lsh.query(minhashes[0])
print("Similar to doc0:", result) # Expected: ['doc0', 'doc1']Example 2: Random Projection LSH (Web Demo)
Simulate LSH with 2D points:
<!DOCTYPE html>
<html>
<head>
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/1.4.2/p5.min.js"></script>
</head>
<body>
<script>
let points = [], buckets = {};
function setup() {
createCanvas(400, 400);
for (let i = 0; i < 50; i++) {
points.push({x: random(0, 400), y: random(0, 400)});
}
}
function draw() {
background(220);
buckets = {};
let v = {x: random(-1, 1), y: random(-1, 1)};
for (let p of points) {
let hash = Math.sign(p.x * v.x + p.y * v.y);
buckets[hash] = buckets[hash] || [];
buckets[hash].push(p);
fill(hash > 0 ? 'red' : 'blue');
circle(p.x, p.y, 5);
}
text(`Buckets: ${Object.keys(buckets).length}`, 10, 20);
}
</script>
</body>
</html>Different LSH Function
Below explained are the many different LSH functions that are used for different use cases and data types.
Bit Sampling LSH
Bit sampling is one of the simplest and cheapest LSH functions. It is associated with the Hamming distance. Given two n-length vectors x and y, the Hamming distance d(x,y) is the number of bits that are different between the two vectors.
Bit sampling is an LSH family where:
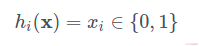
The collision probability is simply the chance that we picked one of the indices where xi=yi :
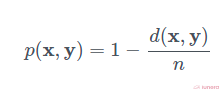
Euclidean and Manhattan LSH
The LSH functions for the Euclidean (L2) and Manhattan (L1) distances are based on random projections that separate the data space into multiple pieces.
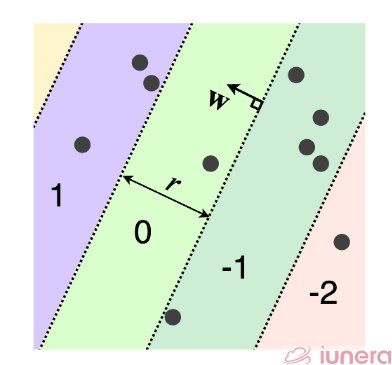
Each piece then becomes a hash bin. The hash function is identical to another algorithm called signed random projections (not stated here), but we round instead of taking the sign of the projection.
This produces hash bins that repeat in the direction of w instead of a single decision boundary as with SRP.
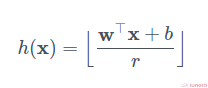
r refers to a user-defined parameter that determines each hash bin’s width, b is a random number in the range [0, r]. The analytic expression for the collision probability is complicated to write down.
Clustering LSH
Clustering LSH is an example of a learned or data-dependent LSH function. The idea is to find a set of cluster centres that do a good job of approximating the data points in the datasets.
The individual centres might be found using k-means clustering, convex clustering, or any other clustering method. It is easy to show that this function is locality-sensitive but much harder to specify the collision probability since collisions depend on the set of learned cluster centres.
Hierarchical Clustering could also be used in certain use cases, and it is proven that it is much faster than the typical brute-force method.
Applications of LSH
Let us take a look at some of the commonly used applications of LSH.
- Near Duplication Detection – LSH is commonly used to deduplicate large quantities of documents, webpages, and other files
- Genome Study – LSH can be used to identify similar gene expressions in genome databases
- Image and Video Search – Large-scale searching can be deployed using LSH
- Video Fingerprinting – In multimedia technologies, LSH is widely used as a fingerprinting technique A/V data
- Recommendation Systems – Matches users/items (e.g., Spotify)
- Multimedia Search – Clusters images/audio (e.g., Shazam)
- iunera Use Case – Optimizes transit by clustering big data mobility data to detect rides
There are two ways an LSH can speed things up: by helping you deal with a vast number of points or by helping you deal with points in a high-dimensional space such as image or video data.
One of the popular music streaming applications, Shazam, uses some advanced music information retrieval techniques to achieve this but one can implement such music recognition for fun using Audio Fingerprinting and Locality Sensitive Hashing.
Audio fingerprinting is the process of identifying unique characteristics from a fixed duration audio stream. Such unique characteristics can be identified for all existing songs and stored in a database.
LSH vs. KD-Trees
| Aspect | LSH | KD-Trees |
|---|---|---|
| Query Time | Sub-linear (e.g., O(log n)) | O(log n) low dims, O(n) high |
| Dimensionality | Scales to high dims | Struggles above 10-20 dims |
| Accuracy | Approximate | Exact |
LSH vs. Vector Databases
| Aspect | LSH | Vector Databases (e.g., Faiss) |
|---|---|---|
| Implementation | Algorithm | Full system with indexing |
| Speed | Fast ANN | Optimized ANN + exact options |
| Flexibility | Requires custom tuning | Pre-built, user-friendly |
- LSH: Core algorithm, often embedded in vector databases.
- Vector Databases: Like Faiss or Pinecone, they enhance LSH with indexing and scalability features.
Recap
Let us recap what has been introduced in the article. Locality Sensitive Hashing (LSH) refers to a set of algorithmic techniques used to speed up the search for neighbours or duplicate data in the samples.
LSH can be applicable to literally any kind of data and how much it’s relevant in today’s world of big data.
LSH functions are specifically designed so that hash value collisions are more likely for two input values close together than for inputs that are far apart. The fundamental intuition behind LSH is that LSH functions try to group similar elements into hash bins.
Conclusion
LSH is a game-changer for similarity search, blending speed and scalability. This guide, with its interactive examples and deep insights, equips you to leverage LSH effectively. At iunera, we harness LSH for smarter solutions—reach out to see how it can transform your data challenges.
Are you looking for ways to get the best out of your data?
If yes, then let us help you use your data.
Related Posts
What is Locality-Sensitive Hashing (LSH)?
LSH is a technique for fast similarity search, hashing similar items into the same bucket with high probability.
How does LSH work?
It uses hash functions where similar items collide more often, reducing the search space.
What are the benefits of LSH?
It’s fast, scalable, and efficient for high-dimensional data.
What are the limitations of LSH?
It’s approximate and requires parameter tuning.
How is LSH different from regular hashing?
Regular hashing avoids collisions; LSH encourages them for similar items.
What are LSH applications?
Recommendation systems, duplicate detection, multimedia search, genomics.
Is 'local sensitive hashing' the same as LSH?
Yes, it’s a common misspelling of Locality-Sensitive Hashing.
How does LSH compare to KD-Trees?
LSH scales better for high dimensions; KD-Trees are exact but slower in high dims.
How does LSH fit into vector databases?
It’s a core ANN method, enhanced by systems like Faiss for scalability.
Can LSH be used with Python?
Yes, libraries like datasketch make it accessible (see examples).
What’s the math behind LSH?
It uses probabilistic hash functions with higher collision rates for similar items.
Why use LSH over exact methods?
It’s faster for large datasets where exactness isn’t critical.
How do I tune LSH parameters?
Adjust ( k ) (hash functions) and ( L ) (bands) for recall/precision.
What are different LSH variants?
MinHash, SimHash, Random Projection, p-Stable, Multi-Probe, Entropy-Based.
How does LSH handle high-dimensional data?
It reduces dimensionality via hashing, maintaining similarity.
Can LSH be used for images?
Yes, with SimHash or Random Projection for feature vectors.
What’s the difference between MinHash and SimHash?
MinHash uses Jaccard similarity; SimHash uses cosine similarity.
How does LSH improve recommendation systems?
It quickly finds similar users/items for suggestions.
